What is Data Representation and Complements ?

 DATA REPRESENTATION : 

Internally the basic building block for digital computers is BIT.

What is Bit ?

Bit is a binary digit .they are 1 and 0 .

Relation Between Bits & Bytes :

nibble = 4 bits

bytes  = 2 nibble or 8 bits

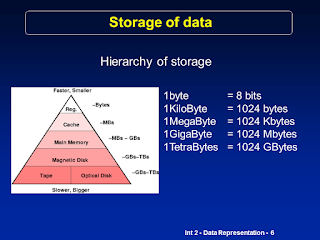
1KB (KiloByte) = 1024 bytes

1MB(MegaByte) = 1024 KB

1 GB(GigaByte) = 1024 MB

1TB(TeraByte) = 1024 GB

1PB(PetaByte) = 1024 TB

1EB(ExaByte) = 1024 PB

1ZB(ZettaByte) = 1024EB

1YB(YottaByte)  = 1024 ZB

1 BB(BrontaByte) = 1024 YB

1 GB(GeopByte) = 1024 BB

Normally a single charecter/number/element is represented in term of one  or more bytes.

COMPLEMENTS :

We are already dealt with possitive  binary numbers. However computer not only handles possitive binary numbers but also negative once.There are three method to represents the negative numbers-

(1)Sign magnitude representation

(2)1's (ones) compliments representation

(3)2's (seconds)compliments representation

Sign Magnitude representation : 

In sign magnitude representation first bit of bytes sign nit and rest represents the number.

1 in sign bit represents the negative numbers

0 in sign bit represents the possitive numbers

Representation of +4 & -4

 

1's (ones)Complement Representation :

ones complement representation of number in binary  is actually result of subtracting one from consecutive one's.

ones complement of 7 in 4 bit representation

1111-0111=1000

or simply inverting 0 to 1

0111---->1000

The prime disadvantage of ones complements that it has two representation of zero

2'S Complements Presentation :

Two's complement is a mathematical operation on binary numbers, and is an example of a radix complement. It is used in computing as a method of signed number representation.

The two's complement of an N-bit number is defined as its complement with respect to 2^N; the sum of a number and its two's complement is 2^N. For instance, for the three-bit number 010, the two's complement is 110, because 010 + 110 = 8 which is equal to 2³. The two's complement is calculated by inverting the digits and adding one.

Three-bit signed integers

Decimal value	Two's-complement representation
0	000
1	001
2	010
3	011
−4	100
−3	101
−2	110
−1	111

Eight-bit signed integers

Decimal value	Two's-complement representation
0	0000 0000
1	0000 0001
2	0000 0010
126	0111 1110
127	0111 1111
−128	1000 0000
−127	1000 0001
−126	1000 0010
−2	1111 1110
−1	1111 1111

Two's complement is the most common method of representing signed integers on computers,^[1] and more generally, fixed point binary values. In this scheme, if the binary number 010₂ encodes the signed integer 2₁₀, then its two's complement, 110₂, encodes the inverse: −2₁₀. In other words, to reverse the sign of most integers (all but one of them) in this scheme, you can take the two's complement of its binary representation. The tables at right illustrate this property.

Compared to other systems for representing signed numbers (e.g., ones' complement), two's complement has the advantage that the fundamental arithmetic operations of addition, subtraction, and multiplication are identical to those for unsigned binary numbers (as long as the inputs are represented in the same number of bits as the output, and any overflow beyond those bits is discarded from the result). This property makes the system simpler to implement, especially for higher-precision arithmetic. Unlike ones' complement systems, two's complement has no representation for negative zero, and thus does not suffer from its associated difficulties.